可编辑网格的存储方式

2018年1月14日 | Oscar | 图形理论

可编辑网格的存储方式

渲染时使用的数据结构往往是数组，因为它节约存储空间而且方便索引进行随机访问。但是在模型编辑软件如 Blender、MAYA 中就不能使用数组，取而代之的是类似于链表的数据结构。
为了方便修改，网格信息时一般不只存储顶点信息，往往还会保存连接信息（mesh connectivity）。

邻接三角形结构

这次要讨论的是邻接三角形结构（The Triangle-Neighbor Structure）。

Triangle {
    Triangle nbr[3];
    Vertex v[3];
}
Vertex {
    // ... per-vertex data ...
    Triangle t; // any adjacent tri
}

邻接三角形一般采用如下形式：

定义一个三角形，三角形里存储指向相邻三个三角形的指针，和指向三个顶点的指针。
定义顶点，顶点里存储属性信息和一个指向任意邻接三角形的指针。

顶点引用图

如图所示：Triangle.nbr中第k个元素，指向和该三角形共享k和k+1顶点的相邻三角形。

一个网格（mesh）包含许许多多这样的信息，在邻接三角形结构下，网格可以用如下方式组织：

Mesh {
    // ... per-vertex data ...
    int tInd[nt][3]; // vertex indices
    int tNbr[nt][3]; // indices of neighbor triangles
    int vTri[nv]; // index of any adjacent triangle
}

网格中除了必须的顶点索引外，还包含两个附加的数组：一个用来存储每个三角形的三个邻接三角形，一个用来存储每个顶点的任意一个邻接三角形。如下图所示：

网格存储示例

在邻接三角形结构的网格中，不仅可以以常数时间找到指定的任何编号好的顶点或者三角形，同时也保持了顶点网格的连续性（connectivity）。

如果顶点 v 是三角形 t 的第 k 个顶点，则 t.nbr[k] 是延顺时针方向围绕着顶点 v 的下一个三角形。如以下伪代码：

TrianglesOfVertex(v) {
    t = v.t
    do {
        find i such that (t.v[i] == v)
        t = t.nbr[i]
    } while (t != v.t)
}

以上算法可以在常数时间内找到所有围绕着顶点 v 的三角形。但是这个算法有一个缺点，由于定义的是 v 指向任意一个三角形（实际也难以规定指向哪一个三角形）。搜索时就会发现必须遍历三角形的顶点来确认自己的位置，产生了许多无意义的搜索。

为了解决这个问题，可以存储指针指向该三角形的特定边缘，而非指向整个邻接三角形。

Triangle {
    Edge nbr[3];
    Vertex v[3];
}
Edge { // the i-th edge of triangle t
    Triangle t;
    int i; // in {0,1,2}
}
Vertex {
    // ... per-vertex data ...
    Edge e; // any edge leaving vertex
}

对于这种结构，每个 vertex 存储四个索引（三个顶点和一条边），每个三角形存储六个索引（三个顶点和三条边）。统计中三角形个数大概是顶点数的两倍，所以所以每个顶点存储占用 4nv + 6nt = 16nv。（nv是顶点个数，每个顶点占用4个基本元素的大小，基本元素大小一般为vec4）。

在这种结构下可以保存进入三角形的信息：

    t.nbr[j].t.nbr[t.nbr[j].i].t == t

也就可以遍历以顶点为中心的三角形：

TrianglesOfVertex(v) {
    {t, i} = v.e;
    do {
        {t, i} = t.nbr[i];
        i = (i+1) mod 3;
    } while (t != v.e.t);
}

对于非完备的三角形网格，则可以对边界三角形没有邻接三角形的边 e，使 e 指向的三角形序号为哨兵即可。

翼边结构

接下来是翼边结构（The Winged-Edge Structure），这种数据结构将边作为最主要的存储单元。

在翼边网格中，每个 edge 存储指向它连接的两个 vertex （头和尾顶点）的指针，它是两个 face （左右面）的一部分，还有四个指针指向左侧和右侧的 lprev，rprev，lnext，rnext，相对中心边，指向边的排序采用逆时针方式，如下所示：

Edge {
    Edge lprev, lnext, rprev, rnext;
    Vertex head, tail;
    Face left, right;
}
Face {
    // ... per-face data ...
    Edge e; // any adjacent edge
}
Vertex {
    // ... per-vertex data ...
    Edge e; // any incident edge
}

翼边示例

相对 e0 而言，e2 为 lprev，e1 为 lnext，e3 为 rnext，e4 为 rprev。

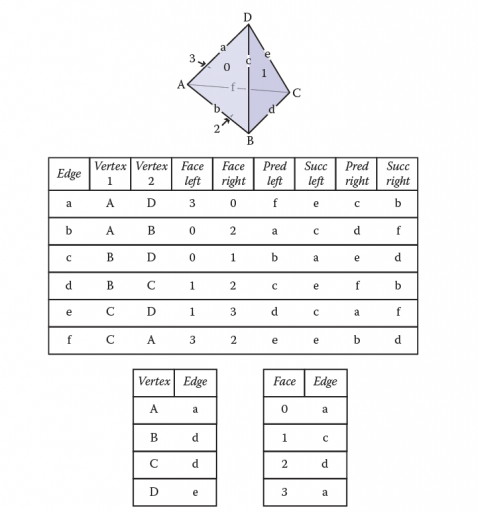
四边形示例

翼边结构可以以常数时间访问当前当前 vertex 或 face 的所有相邻边。

EdgesOfVertex(v) {
    e = v.e;
    do {
        if (e.tail == v)
            e = e.lprev;
        else
            e = e.rprev;
    } while (e != v.e);
}

EdgesOfFace(f) {
    e = f.e;
    do {
        if (e.left == f)
            e = e.lnext;
        else
            e = e.rnext;
    } while (e != f.e);
}

与邻接三角形结构不同的是：翼边结构在多边形也同样适用。

翼边结构也可以去掉 prev 分量，但是如此的话，想要获取 prev 边就必须循环遍历整个 face 来获取它。具体选择要根据空间与时间的平衡。

半边结构（The Half-Edge Structure）

翼边结构相当优雅，但是它仍有一个可以改进的地方——它需要在移动到下一个边缘之前该 edge 的方向。采用半边结构可以解决这个问题。

数据存储在每个 edge 分割而成的两个 half-edges 上。每一个 half-edge 会包含四个指针，一个指向它的面元 face，一个指向该 half-edge 的头顶点（head vertex），一个指向另一个相反的 half-edges ，一个指向逆时针旋转的下一条 half-edge。和翼边结构类似，半边结构也可以不保存指向同直线 half-edge 的指针。结构代码如下所示：

HEdge {
    HEdge pair, next;
    Vertex v;
    Face f;
}
Face {
    // ... per-face data ...
    HEdge h; // any h-edge of this face
}
Vertex {
    // ... per-vertex data ...
    HEdge h; // any h-edge pointing toward this vertex
}

图例如下所示：
半边结构图例

遍历半边结构也与遍历翼边结构类似，除了——不在需要检查方向。

EdgesOfVertex(v) {
    h = v.h;
    do {
        h = h.pair.next;
    } while (h != v.h);
}

EdgesOfFace(f) {
    h = f.h;
    do {
        h = h.next;
    } while (h != f.h);
}

这次遍历 vertex 的方向是顺时针的，因为省略了指向 prev 的指针。

半边结构的存储示例：

在没有边界的网格中，半边通常成对存在，所以很多实现都可以去掉 pair 指针。通过布置阵列，是的偶数边缘 i 总是和 i + 1 配对，奇数边缘 j 总是和 j – 1 配对。

所有这三种网格拓扑结构都可以支持各种类型的网格进行修改，例如分割或折叠顶点，交换边缘，添加或删除三角形等。具体取用哪一个都需要进行分析后选择。