蒙特卡罗综述
许多事情在生活中太难以评估,特别是当它涉及非常大的数字。例如,计算一个国家的成年人口的平均高度,将需要测量每个人的身高,身高值相加除以总人数。这明显是不可能的,这种任务需要很长的时间,非常难以求解。在这种情况下,可以做的是取一个样本的人口并计算其平均高度,以此来估算整个国家人口的平均高度。这是统计学中最简单的概念。
需要特别提醒的是,在这个例子中,随机选取的人的身高是随机数,样本地区身高总和是随机数,连取得样本的平均身高也是随机数。因此,在数学上,全国人口的身高可以被称为随机变量(random variable),一般以大写来表示;组成全国人口的个人的身高被称为样本,它也是随机的(虽然在我们看来某一个人的身高是固定的,但它可以看做是一个随机器产生的结果),一般用小写来表示。
可以使用如下公式来表示随机变量和样本的关系:Approximation(Average(X)) = { 1 \over N} \sum_{n=1}^N x_n 可以看出,随机变量 X 的平均值近似等于选取的 N 的样本的总和除以总数 N,也就是所说的蒙特卡洛估计( Monte Carlo approximation),蒙特卡洛估计就是用样本来估计总体的属性。
已知所有样本的属性求平均叫数学期望( mathematics expectation)。E(X) \approx { 1 \over N } \sum_{n = 1}^N x_n 在很多情况下不能行之有效地精确计算期望值,MC 就可以提供了一种非常简单和快速的方式来近似该期望,它无法给你确切的值,但它可以足够接近期望,而且只需要消耗一小部分资源。
蒙特卡罗积分与有偏以及无偏光线追踪
如果要计算 16×16 像素图片的平均颜色,尽管可以直接求平均。但这并不是普适性的,因为图片的像素值可能很大,图片的量也可能很多。一种方法是随机选择8个点,使用 8 个点的平均来估计确切的平均值。
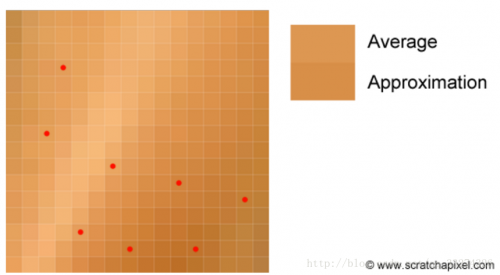
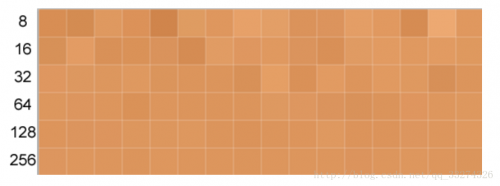
虽然可以通过增加采样点数降低误差,但是为了消除一半的误差,样本数需要增加二倍。这就说明采用蒙特卡洛方法的收敛率是非常低的——当误差小到一定程度,再想减少,需要的样本数会急剧增加。以下是分别采样 8、16、32、64、128、256 的结果:

因为评估蒙特卡洛积分采用的方法是光线追踪,所以这种方法也叫做蒙特卡洛光线追踪。
三篇介绍蒙特卡洛光线追踪的论文:
The Rendering Equation (Kajiya 1986)
Stochastic Sampling in Computer Graphics (Cook 1986)
Distributed Ray-Tracing (Robert L. Cook, Thomas Porter, Loren Carpenter 1984)
接下来介绍什么是有偏和无偏。
统计学中计算期望的大约计算称为估计(estimator),如下所示:Approximation(E(X)) = { 1 \over N } \sum_{n=1}^N x_n 这被称为基本估计,事实上也是简化版的蒙特卡洛估计。当样本数量 N 上升时,估计逐渐逼近期望,就称为无偏估计,当 N 增长到无限大时,估计值会收敛为一个固定值。另一种写法是当估计值和期望在 N 趋于无穷大时逼近于0:Approximation(E(X)) – E(X) = 0 \text { as N approaches } \infty 这就是实际的蒙特卡洛估计,蒙特卡洛估计是一个无偏估计。
当估计值在 N 趋于无穷大时不收敛于 0 的估计就称为有偏估计,但有偏估计不是说不会收敛到一个固定值,可能只是没有收敛到期望值。乍一看可能觉得无偏估计比有偏估计更好,但在很多情况下在样本数相同时有偏估计的收敛速度比无偏估计收敛得更快,而这时候和无偏估计的偏差可能是无法察觉的。
下面可以拓展一下蒙特卡洛光线追踪的概念。
根据光照理论,表面上一点的入射光强度等于出射光强度,即L_P = \int_\Omega L_\Omega 其中 \Omega 表示积分半球。
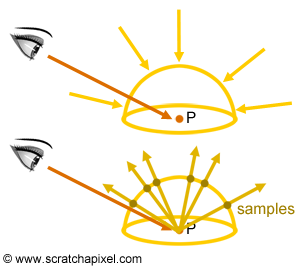
如果采用像往常一样的方法试图分析,将损耗巨大。在这里可以使用蒙特卡罗积分,在半球上随机采样,再由 P 点发出光线,估计有多少光照到达了 P 点,即L_P \approx { 1 \over N } \sum_{n=1}^N L_n
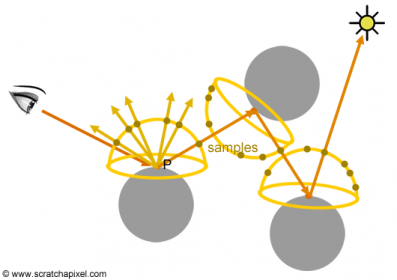
这是蒙特卡洛光线追踪器通常的工作。当 P 点向场景再次发出光线,这条光线仍然可以和其他物体相交,从而递归下去,这种方法也叫做路径追踪(path tracing)。
下面是路径追踪的伪代码示意:
Vec3f monteCarloIntegration(P, N)
{
Vec3f lightAtP = 0;
int nsamples = 8;
for (int n = 0; n < nsamples; ++n) {
Ray sampleRay = sampleRayAboveHemisphere(P, N);
Vec3f Phit;
Vec3f Nhit;
if (traceRay(sampleRay, Phit, Nhit)) {
lightAtP += monteCarloIntegration(Phit, Nhit);
}
}
lightAtP /= nsamples;
return lightAtP;
}
void render()
{
Ray r;
computeCameraRayDir(r, ...);
Vec3f Phit;
Vec3f Nhit;
if (traceRay(r, Phit, Nhit)) {
Vec3f lightAtP = monteCarloIntegration(Phit, Nhit);
...
}
}
最后,蒙特卡洛方法是基于随机采样的数值技术,用于估计结果,特别是积分结果。蒙特卡洛方法是渲染领域的绝对核心,它和许多重要领域密切相关,如采样,重要性采样,光传输算法,以及许多着色算法等等。
本文翻译整理自 A Quick Introduction to Monte Carlo Methods。